近日,重点实验室的蒋建华教授与北欧理论物理研究所的Adrien Bouhon,剑桥大学卡文迪许实验室的Robert-Jan Slager团队合作,在基于声学谐振腔耦合的声子晶体中实现了非阿贝尔拓扑半金属及其相变。相关工作以Experimental observation of non-Abelian topological acoustic semimetals and their phase transitions为题发表于期刊Nature Physics。苏州大学蒋建华教授与剑桥大学的Robert-Jan Slager、北欧理论物理研究所的Adrien Bouhon 为论文的共同通讯作者,苏州大学硕士生姜斌、博士生林志康和北欧理论物理研究所的Adrien Bouhon为本文的共同第一作者。苏州大学的侯波教授、博士生周萧溪,北京理工大学的李锋教授参与了讨论,并对实验进行了指导。
随着对称性保护的拓扑相出现,近几年人们对拓扑物态的分类取得了快速进展。分析在高对称动量空间中能带变换的方式,我们可以推导出相容性关系:在给定对称性的晶格上,可以确定有多少种不同的带隙打开的能带结构。此外,通过比较实空间轨道,我们可以分辨出哪些拓扑类可以等同为平庸的阻碍原子极限的拓扑。在这种框架下,拓扑不变量由单带隙表征,并且可叠加,例如,拓扑不变量来自于费米能级以下每一组能带的叠加贡献。
最近,人们从理论上预测和研究了超出上述范式的拓扑相。为了刻画这种拓扑相,人们提出了描述多带隙希尔伯特空间拓扑的非阿贝尔拓扑不变量,例如四元数框架电荷,最终形成了新的不变量,例如欧拉类(Euler class)。与传统不变量相比,这种拓扑不变量可以在相邻带隙中的结点编织上进行转换,反映了一种全新的拓扑现象。由于缺乏合适的实验系统,迄今为止,非阿贝尔半金属及其相变尚未得到证实。
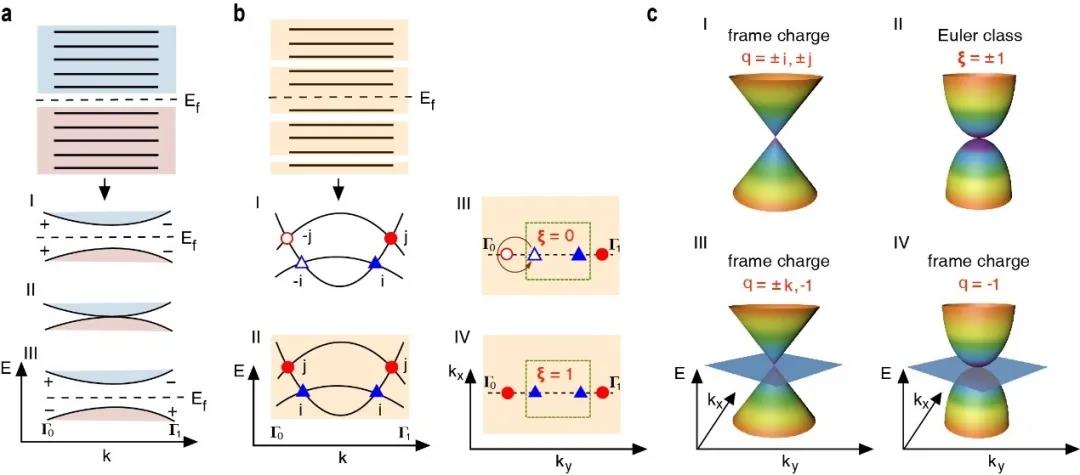
图1. 传统单带隙拓扑玉多带隙非阿贝尔拓扑相比较。(a)传统的(阿贝尔)拓扑不变量定义在单个带隙上,通过能带反转(Ⅱ),从平庸绝缘体(Ⅰ)转变从拓扑绝缘体(Ⅲ)。(b)非阿贝尔能带拓扑定义在多带隙系统,它的拓扑不变量依赖于相邻带隙能带结点之间的编织。(c)非阿贝尔拓扑结点:(Ⅰ)狄拉克点框架电荷为 或者。(Ⅱ)二次型结点欧拉类为ξ=±1。(Ⅲ)线性三重简并点框架电荷为或者-1。(Ⅳ)二次型三重简并点框架电荷为。
根据同伦群论,能带结点的框架电荷q与SO(3)/D2有关,在四元数群的共轭类中取值,例如。四元数群中,基础元素的基本乘法规则为和。
注意,在四元数群中q = 1代表平庸框架电荷。
不像单带隙拓扑不变量(例如缠绕数),这里每一个结点的框架电荷依赖于相邻带隙结点的编织。如图1b,第1带隙中一个狄拉克点(框架电荷为- i与其周围第2带隙中另一狄拉克点(框架电荷为-j)编织,这两个结点框架电荷的符号改变,分别变为i和j。然后第一和第二带隙中的结点变得稳定,即每个带隙中具有相同的框架电荷。相比之下,在编织前,在第一(二)带隙中的两个能带结点拥有相反的框架电荷q=±i(±j),它们能成对湮灭。这种湮灭的阻塞可以用一个拓扑不变量来量化,叫做欧拉类,它可以在包含该两能带子空间所有结点的布里渊区任何区域上定义。这个不变量依赖于涉及到两个带隙的编织过程,因此代表了一种新的不变量。
在图1b中,q=±i(±j)描述了第一(二)带隙中的线性结点。它们是狄拉克锥,如图1c所示。当两个具有相同框架电荷的线性结点合并时,例如q = j,它们形成一个框架电荷q = -1,q = -1区域欧拉类(见图1c)的稳定二次型结点。上述图景暗示了Nielsen-Ninomiya理论的非阿贝尔规避,该理论指出只有总阿贝尔电荷为0的结点才能在单一带隙中同时产生或湮灭。相反,在非阿贝尔半金属中,具有相反框架电荷的结点,总电荷q= i *(-i) = j *(- j)=1,能同时产生或湮灭。而其余所有情形均为拓扑稳定的。
此研究理论上提出实验上证实了一种2D kagome声学超材料可以作为优异的材料平台用来研究非阿贝尔拓扑相。在这种超材料中,通过调节两个几何参数,可以有效操纵声学布洛赫能带。通过调节这些几何参数,在多带隙系统中演示了能带结点以及非阿贝尔拓扑荷的演化。能带结点的非阿贝尔拓扑荷能够转换,甚至能从一个带隙转移到另一个带隙。在演化过程中,发现了丰富的非阿贝尔相变,包括在远离布里渊区中心处一对狄拉克点合并产生二次型结点,具有三重简并点和不可避免的中间相在结点从一个带隙转移到另一个带隙中起了重要作用。通过互补的理论、计算和实验,揭示了拓扑结点产生、湮灭、合并和分裂的规则,能够转换和在带隙间转移的非阿贝尔拓扑荷是系统多带隙结构作用的结果。更进一步,此研究观测到了多带隙拓扑边界态,揭示了边界态可以作为体中非阿贝尔拓扑结点演化的替代探针。
此研究从一个精心设计的模型出发,该模型通过晶体对称性的复杂相互作用来阐明这种多带隙物理。考虑一个紧束缚模型,具有可调的最近邻耦合和次近邻耦合,分别用t和t’标记(见图2a)。每一个原胞中三个子格点,分别用A,B和C标记。每一个格点有1条s轨道,由于C2T对称性,形成一个由实值哈密顿量描述的三能带系统。通过调节最近邻和次近邻耦合,可以触发第一和第二带隙中能带结点的演化,如图2b-2h。
首先,当非阿贝尔电荷在两个带隙中转换和转移,演化过程包含结点的产生、湮灭、合并和分裂,这一特征不能通过传统的拓扑能带理论来理解,坚定地揭示了多带隙拓扑的非阿贝尔特性。此研究强调,三重简并点的产生对非阿贝尔电荷在两个带隙中的转移起了至关重要的作用。第二,线性三重简并点的产生与K和K’ 处的二次型结点不能用对称性分析来解释,而是源于固有的非阿贝尔能带拓扑。第三,在该模型中,非阿贝尔电荷通常与结点色散有关。图1c和图2所示,带隙I(II)中的狄拉克点对应的框架电荷为q=±i(q = ±j)。二次型结点框架电荷q = -1,同时具有欧拉类.然而,三重简并点是独特的。例如,它们没有欧拉类,但框架电荷为q=±k或者-1。另外,线性和二次型的色散能有相同的框架电荷 q=-1。
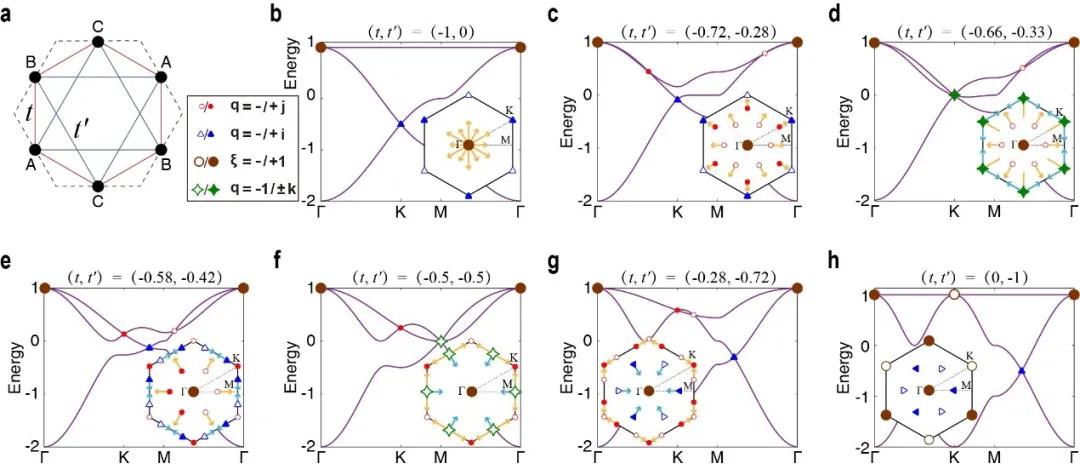
图2. 非阿贝尔拓扑能带结点及其演化。(a)Kagome紧束缚模型。(b-h)能带结构(主图)和带隙Ⅰ和Ⅱ中结点(插图)的演化。
为了在实验中研究非阿贝尔拓扑相,此研究设计了一种kagome声学超材料,重现了紧束缚模型中所有的显著特征。图3d-3i显示,实验测量的声学能带结构与计算结果相吻合,尤其是当考虑到声波的固有耗散和有限尺寸效应。在插图中呈现了计算的能带结点分布以及它们的非阿贝尔拓扑荷。图3中实验与计算的一致性证实了带隙I和II中结点的产生、移动、合并和分裂。因此,图3的结果为非阿贝尔拓扑半金属及其相变提供了直接证据。观测结果也为受晶体对称性限制和遵循基本演化规则的非阿贝尔拓扑荷在不同带隙之间的转换和转移提供了间接证据。
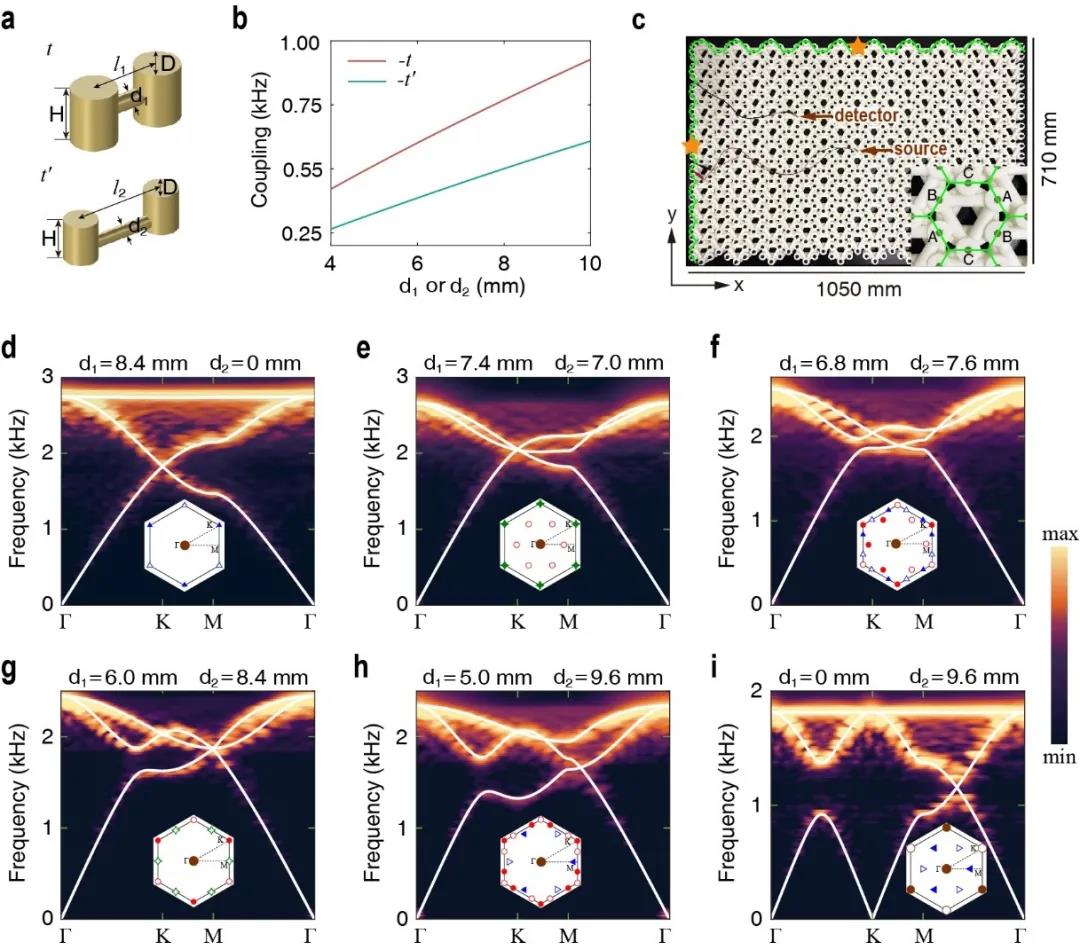
图3. Kagome声学超材料和非阿贝尔拓扑结点。(a)圆柱形声学谐振腔来构建Kagome格子;最近邻(次近邻)耦合用水平管来实现。(b)改变直径调节最近邻和次近邻耦合。(c)测量体能带和边界态结构的实验装置照片。(d-f)超材料的声学能带结构。
从体的拓扑荷构型及其演化,此研究观测到边界态在编织过程中的演化。反过来,边界态的演化间接地反映了能带结点体的编织。拓扑能带结点对两个带隙I和II的边界态有直接影响。在每一个带隙中,对于沿边缘边界的给定动量,可以定义Zak相。对于锯齿状边界,Zak相是量子化的,并在经过奇数个狄拉克点时从0与π之间相互切换。因为一个二次型结点等价于两个狄拉克点,它对Zak相没有影响。另一方面,一个框架电荷q=±k(q=-1)的三重简并点,在两个带隙I和II中都等价于奇数(偶数)个狄拉克点。对于实验中所研究的边界态,Zak相为π(0)导致出现(缺失)边界态。因此,边界态的出现和缺失反映了能带结点在布里渊区边界的投影。利用声学系统不受费米-狄拉克填充效应的优点,此研究测量两个带隙I和II的边界态,研究多带隙体边物理。
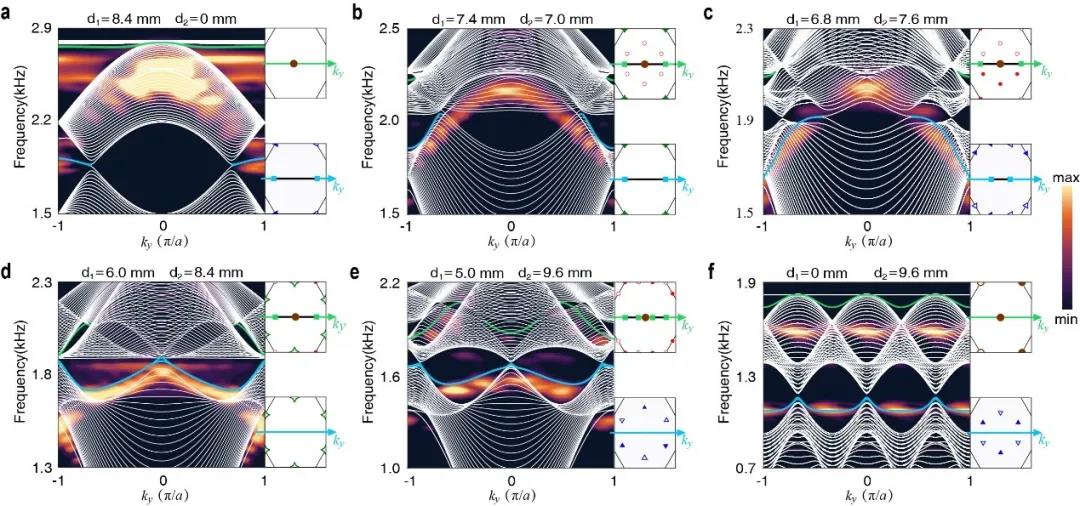
图4. Kagome声学超材料中的多带隙体边物理。(a-f)实验测量超材料的锯齿状边界态声学色散。
由于与Kagome对称性的相互作用,此研究理论上预测了具有新的多带隙可观测的简单模型。更重要的是,利用这些结果和Kagome声学超材料中的声学布洛赫能带,从实验上观测到了非阿贝尔拓扑半金属及其演化。此研究从实验上证实了拓扑能带结点在多个带隙中的产生、湮灭、移动、合并和分裂,和与之相关的非阿贝尔拓扑相变(例如,非阿贝尔电荷在不同带隙间的转换和转移)。能带结点非阿贝尔拓扑荷演化和转换的基本规律对于理解具有多个相互连接能带的拓扑半金属、中心反演-时间反演对称系统中的淬火动力学以及非平衡玻色子系统中的多带隙拓扑现象具有重要意义。
原文链接:https://www.nature.com/articles/s41567-021-01340-x
